4851. Details
The company “Auto-2012” produces
engines for world-famous cars. The engine consists of exactly n details, numbered from 1 to n, while the detail with the
number i is manufactured
for pi seconds.
Specificity of the enterprise “Auto-2012” is that only one engine component can
be manufactured at a time. To produce some details, you must have a pre-made
set of other details.
The general director of “Auto-2012”
set before the company an ambitious task – for the shortest time to make the
detail number 1 to present it at the exhibition.
Write a program that,
according to the given dependences of the order of production between the
details, finds the shortest time for which you can make a detail with
number 1.
Input. The first line contains n (1 ≤ n ≤ 105) integers p1, p2, ..., pn giving the manufacturing time of each detail in seconds.
Each of the following n lines describes the characteristics of
the details production. Here i-th
line contains the list of details that are required for the production of the
detail with the number i. There are
no duplicate detail numbers in the list. The list can also be empty – then it will have an empty
string! The sum of the lengths of all lists does not exceed 200000.
It is known that there are
no cyclical dependencies in the production of details.
Output. Print the minimum time (in
seconds) required for the speedy production of the detail with number 1.
|
Sample input 1 |
Sample output 1 |
|
100
200 300 2 2 1 |
300 |
|
|
|
|
Sample input 2 |
Sample output 2 |
|
3 5 1 2 3 1 4 4 |
6 |
SOLUTION
graphs – topological
sort
Algorithm analysis
Let’s construct a graph of details dependencies and
reverse it. To produce the detail number
1, you must produce all the details reachable from it (the first detail depends from all of them). Detail i is produced in pi seconds, assign
the weight pi to the i-th vertex.
Start a depth first search
from the vertex 1
and compute the sum
of weights of all vertices reachable from it (including 1). This will be
the required minimum time.
Example
Consider the first example.
Let’s construct a graph of details’ dependencies
(on the left) and its inverse graph (on the right).
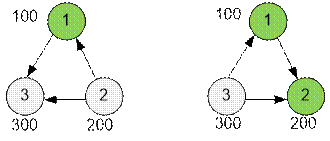
The first detail
depends on the second. The second detail does not depend on any other. In the
reverse graph from the first vertex there is a path only to the second. Therefore, the
total time through which the first detail can be produced is 100 + 200 = 300 (first
we produce the
second detail, then
the first).
Consider the
second example: a graph and its inverse.
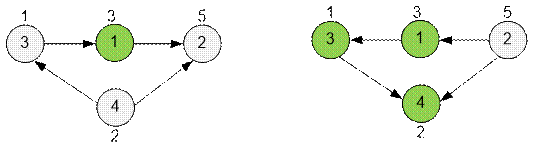
In the reverse
graph, the path from the first vertex exists to 3 and 4. The time after which the first
detail can be
produced is 3 + 1 + 2 = 6.
Algorithm realization
Store the time of
manufacturing details in the array p.
#define MAX 100010
long long p[MAX];
Declare a
graph g and an array used of visited vertices during the depth first search.
int
used[MAX];
vector<vector<int> > g;
Function
dfs
implements depth first search. For the detail (vertex) v we compute the shortest time after which it can be
produced. It equals to the
immediate production time of the detail p[v]
plus the production time of the details which v depends from. Details are produced by one device – one by one, not in
parallel.
long long dfs(int v)
{
used[v] = 1;
long long res = p[v];
for (int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i];
if (!used[to]) res += dfs(to);
}
return res;
}
The main part of the program. The number of details is not known, read
them till the end
of line, count their number in the variable n.
Store the
production time of the details in the
array p.
n
= 1;
while(scanf("%lld%c",&p[n],&ch), ch != '\n') n++;
Read
the information about dependencies between the order of manufacturing the details.
g.resize(n+1);
for(i
= 1; i <= n; i++)
{
gets(s);
stringstream in(s);
To manufacture the detail number i, all
parts which numbers
are in the line s must be produced. Given a line s, construct a stream in. For each number a from the stream
create an edge i ® a.
while (in >> a)
g[i].push_back(a);
}
Compute and print the shortest time for production the detail number 1.
memset(used,0,sizeof(used));
res
= dfs(1);
printf("%lld\n",res);